കെ ടെറ്റ് /PSC പഠനസഹായി 20( ഗണിതം)

1. സംഖ്യാശ്രേണി

അടുത്തടുത്ത മൂന്നു സംഖ്യകള്‍ തമ്മിലുളള ബന്ധം കണ്ടെത്തി അതിന്റെ അടിസ്ഥാനത്തിലാകണം സംഖ്യാശ്രേണി പൂരിപ്പിക്കേണ്ടത്.

സമാന്തരശ്രേണിയില്‍ അടുത്തടുത്ത സംഖ്യകളുടെ പൊതുവ്യത്യാസമാണ് കണ്ടെത്തേണ്ടത്.

• കൂട്ടുക
• കുറയ്കുക

 സമഗുണിതശ്രേണിയില്‍ ഒരു പ്രത്യേകസംഖ്യകണ്ട് ഗുണിച്ച് പോവുകായാണ് ചെയ്യുക
 മറ്റു ശ്രേണികളുമുണ്ട്. ഒന്നിടവിട്ട് കൂട്ടുക, വര്‍ഗം കാണുക എന്നിങ്ങനെ പലയുക്തി പ്രയോജനപ്പെടുത്തും

• 10,20,32,46------

• (10+10,20+12,30+14, 46+16)

• 2,8, 3,27, 4--- 
  • (2X2X2,3X3X3,4X4X4)

• 6,8,12,7,18,6-- രണ്ടു ശ്രേണികള്‍ ഉണ്ടെന്നു കണ്ടെത്തണം 
  • 6,12,18...24 
  • 8,7,6---5

• 1,3 ,12,60--- 
  • 1X3,3X4,12X5,60X6

• 1,9,25,49..... ( സംഖ്യകളുടെ വര്‍ഗങ്ങളാണ് )
  

2.ചതുരത്തിന്റെ പ്രത്യേകതകള്‍ -

എല്ലാ കോണുകളും എല്ലാ വശങ്ങളും തുല്യമായ ചതുര്‍ഭുജമേത്?

• സമഭുജസമാന്തരികം
• ലംബകം
• സമചതുരം
• ചതുരം

1. ചതുരത്തിന് നാലു വശങ്ങള്‍ ഉണ്ട്
2. ചതുരത്തിന്റെ എതിര്‍വശങ്ങള്‍ തുല്യനീളമുള്ളവയാണ് 
3. ചതുരത്തിന്റെ മൂലകള്‍ തുല്യമായിരിക്കും ( കോണളവ്)
4. ചതുരത്തിന്റെ മൂലയിലെ വശങ്ങള്‍ പരസ്പരം കുത്തനെയയായിരിക്കും 
5. ചതുരത്തിന്റെ മൂലയിലെ വശങ്ങള്‍ പരസ്പരം കുത്തനെയകുമ്പോള്‍ അത് മട്ടമാണ്.
   ചതുരത്തിന്റെ വിസ്തീര്‍ണം = നീളംx വീതി ( ഒരളവു തന്നാല്‍ മറ്റൊന്നു കണ്ടു പിടിക്കുന്ന രീതി ?)
   5x2 =10
   2=10/5
   5=10/2 
   axb=c
   a=c/b
   b=c/a ചതുരത്തിന്റെ ചുറ്റളവ്  =നീളം+വീതിx 2
   ( ഒരളവു തന്നാല്‍ മറ്റൊന്നു കണ്ടു പിടിക്കുന്ന രീതി ?)
   സമചതുരത്തിന്റെ വിസ്തീര്‍ണം= വശം x വശം
   സമചതുരത്തിന്റെ ചുറ്റളവ് =വശംx4
   ഒരു സമചതുരത്തിന്റെ ചുറ്റളവ് 160 മീ. വിസ്തീര്‍ണമെത്ര?
   • 1600
   • 40
   • 160
   • 400

3. ത്രികോണത്തിന്റെ പ്രത്യേകതകള്‍ എഴുതൂ

1. ഏത് രണ്ട് വശങ്ങളുടെ തുകയും മൂന്നാമത്തെ വശത്തേക്കാള്‍ വലുതായിരിക്കും
   2..........................

ടെസലേഷന്‍. സിമിട്രി എന്നിവ അറിയാമല്ലോ

4. സംഖ്യ, ഗുണിതം ഘടകം ,ഗുണനവസ്തുത

• പൊതുഗുണിതം
• ഘടകങ്ങള്‍ - 16 = 1 x 16 = 2 x 8 = 4 x 4 എന്നിങ്ങനെ ഗുണിതങ്ങളായി എഴുതാമല്ലോ. 1, 2, 4, 8, 16 എന്നിവയെ 16-ന്റെ ഘടകങ്ങള്‍ (factors) എന്ന് വിളിക്കുന്നു
• ഭാജ്യ സംഖ്യ , അഭാജ്യ സംഖ്യ
• അഭാജ്യ സംഖ്യ – ഒരു സംഖ്യയെ ഒന്നു കൊണ്ടും അതേ സംഖ്യകൊണ്ടും മാത്രം നിശേഷം ഹരിക്കാനാകുകയുളളുവെങ്കില്‍ അത് അഭാജ്യ സംഖ്യയാണ് (13) കൃത്യം രണ്ടു ഘടകങ്ങള്‍ ഉള്ള സംഖ്യകളെ — ഈ ഘടകങ്ങള്‍ 1-ഉം ആ സംഖ്യതന്നെയും ആയിരിക്കും — അഭാജ്യസംഖ്യകള്‍ അല്ലെങ്കില്‍ അഭാജ്യങ്ങള്‍ എന്ന് വിളിക്കുന്നു. ഉദാഹരണത്തിന് 2, 3, 5, 7 എന്നിവ അഭാജ്യങ്ങളാണ്.
  • 2 = 1 x 2,
  • 3 = 1 x 3,
  • 5 = 1 x 5,
  • 7 = 1 x 7
• ഭാജ്യസംഖ്യ- ഒരു സംഖ്യയെ ഒന്നു കൊണ്ടും അതേ സംഖ്യകൊണ്ടുമല്ലാത്ത മറ്റു സംഖ്യകള്‍ കൊണ്ടും നിശേഷം ഹരിക്കാനാകുന്നുവെങ്കില്‍ അത് ഭാജ്യ (12) സംഖ്യയാണ് 
  • ഭാജ്യസംഖ്യയോ അഭാജ്യ സംഖ്യയോ അല്ലാത്തത്
    • 2
    • 3
    • 4
    • 1
• ഒന്നിനെ ഭാജ്യ സംഖ്യയോ അഭാജ്യ സംഖ്യയോ ആയി പരിഗണിക്കാറില്ല
  • എണ്ണല്‍ സംഖ്യ അഥവാ നിസര്‍ഗസംഖ്യ (1,2,3,4...) 
  • അഖണ്ഡ സംഖ്യകള്‍ (0,1,2,3,4...)
  എണ്ണല്‍ സംഖ്യകളില്‍ ഏറ്റവും ചെറുതേത്?
  • 0
  • 1
  • 2
  • 5
  ഒരക്കമുളള എണ്ണല്‍ സംഖ്യകളുടെ എണ്ണം? 9 . രണ്ടക്കമുളള എണ്ണല്‍ സംഖ്യകളോ?
  താഴെക്കൊടുത്തിരിക്കുന്നവയില്‍ സമ്പൂര്‍ണ സംഖ്യ ഏത്?
   5,6,7,8
  6എന്ന സംഖ്യയുടെ ഘടകങ്ങളില്‍ 6 ഒഴികെ മറ്റുളളവയായ 1,2,3 തമ്മില്‍ കൂട്ടിയാല്‍
  6 തന്നെ കിട്ടും. അങ്ങനെയുളള സംഖ്യകളെയാണ് സമ്പൂര്‍ണ സംഖ്യകള്‍ എന്നു പറയുക

നാലിന്റെ ഗുണിതം

• ഒരു സംഖ്യ നാലിന്റെ ഗുണിതമാണോ എന്നറിയാന്‍ അവസാനത്തെ രണ്ടക്കങ്ങള്‍ ചേര്‍ന്ന സംഖ്യ നാലിന്റെ ഗുണിതമാണോ എന്നു നോക്കിയാല്‍ മതി. 1916

എട്ടിന്റെ ഗുണിതം

• ഒരു സംഖ്യ എട്ടിന്റെ ഗുണിതമാണോ എന്നറിയാന്‍ അവസാനത്തെ മൂന്നക്കങ്ങള്‍ ചേര്‍ന്ന സംഖ്യ 8ന്റെ ഗുണിതമാണോ എന്നു നോക്കിയാല്‍ മതി

ഒമ്പതിന്റെ ഗുണിതം

• ഒരു സംഖ്യ ഒമ്പതിന്റെ ഗുണിതമാണോ എന്നറിയാന്‍ ആ സംഖ്യയിലെ അക്കങ്ങളുടെ തുക ഒമ്പതിന്റെ ഗുണിതമാണോ എന്നു നോക്കിയാല്‍ മതി

മൂന്നിന്റെ ഗുണിതം

• ഒരു സംഖ്യ മൂന്നിന്റെ ഗുണിതമാണോ എന്നറിയാന്‍ ആ സംഖ്യയിലെ അക്കങ്ങളുടെ തുക മൂന്നിന്റെ ഗുണിതമാണോ എന്നു നോക്കിയാല്‍ മതി
• മുകളില്‍ സൂചിപ്പിച്ച കാര്യങ്ങളെ ആധാരമാക്കി നിശേഷം ഹരിക്കാമോ എന്നു കണ്ടെത്താമല്ലോ 
  ഒമ്പതിന്റെ ഗുണിതം
• അക്കങ്ങളുടെ തുക ഒമ്പതിന്റെ ഗുണിതമാണെങ്കില്‍ ഒമ്പതുകൊണ്ട് നിശേഷം ഹരിക്കാം എന്നു കണ്ടെത്താമല്ലോ. അതു പോലെ കണ്ടെത്തലുകള്‍ നടത്തൂ
• രണ്ടുകൊണ്ട് , അഞ്ചുകൊണ്ട്, പത്തുകൊണ്ട് നിശേഷം ഹരിക്കാവുന്ന സംഖ്യകളുടെ പ്രത്യേകതകള്‍ കണ്ടെത്തൂ
  • ഒറ്റയുടെ സ്ഥാനത്ത് ഇരട്ട സംഖ്യ
  • ഒററയുടെ സ്ഥാനത്ത് 0,5
  • ഒറ്റയുടെ സ്ഥാനത്ത് 0
•  ആറുകൊണ്ട് നിശേഷം ഹരിക്കല്‍ഒരു സംഖ്യ രണ്ടുകൊണ്ടും മൂന്നുകൊണ്ടും നിശേഷം ഹരിക്കാമെങ്കില്‍ ആറുകൊണ്ടും നിശേഷം ഹരിക്കാം
•  പതിനൊന്നുകൊണ്ട് നിശേഷം ഹരിക്കല്‍
  ഒന്നിടവിട്ട സംഖ്യകളുടെ തുക തുല്യമോ, വ്യത്യാസം പതിനൊന്നോ പതിനൊന്നിന്റെ ഗുണിതമോ ആണെങ്കില്‍. 5016 ( 5+1=6, 0+6=6 )
  • 3,4ഇവ കൊണ്ട് നിശേഷം ഹരിക്കാവുന്ന ഏതു സംഖ്യയേയും പന്ത്രണ്ട് കൊണ്ടും നിശേഷം ഹരിക്കാം.
  • 5016നെ ഇവയില്‍ ഏതൊക്കെ സംഖ്യകള്‍കൊണ്ട് നിശേഷം ഹരിക്കാം? (2,3,4,6,11,12?)

ഏഴുകൊണ്ട് നിശേഷം ഹരിക്കാമോ?

നിയമം ഒന്ന് തന്നിരിക്കുന്ന സംഖ്യയുടെ അവസാനത്തെ അക്കം മാററിയശേഷം ആ അക്കത്തിന്റെ ഇരട്ടി ബാക്കി സംഖ്യയില്‍ നിന്നും കുറയ്കുക. കിട്ടുന്ന ഫലത്തിലെ അവസാനത്തെ അക്കം വീണ്ടും മാറ്റി പ്രക്രിയ തുടരുക. അവസാനം പൂജ്യം ലഭിക്കുന്നുവെങ്കില്‍ ഏഴുകൊണ്ട് നിശേഷം ഹരിക്കാം.

12264 / 7,

1226 - 8 = 1218

121 - 16 = 105

10 - 10 = 0

12264നെ 7 കൊണ്ട് നിശേഷം ഹരിക്കാം

താഴെക്കൊടുത്തിരിക്കുന്നവയില്‍ നിശേേഷം 36കൊണ്ട് ഹരിക്കാന്‍ കഴിയാത്ത സംഖ്യ ഏത്? ( രണ്ടുതവണ ചോദിച്ചു)

• 91116, 44424, 967484, 93132
• 5258 ,9128, 19512, 25954

താഴെക്കൊടുത്തിരിക്കുന്നവയില്‍ 7,9,12എന്നിവ കൊണ്ടു ഹരിച്ചാല്‍ ശിഷ്ടം 1കിട്ടുന്ന സംഖ്യ ഏത്?

• 253, 352, 509,756

3ന്റെ ഗുണിതമായ ഒരു സംഖ്യയാണ് 2511367208M21 ഇതില്‍ Mനെ സൂചിപ്പിക്കുന്ന സംഖ്യ ഏത്?

• 5,1,4,7

താഴെക്കൊടുത്തിരിക്കുന്നവയില്‍ ഏതു രീതിയാണ് ഗുണനവസ്തുത സ്വായത്തമാക്കുന്നതില്‍ ഗണിതപഠനസമീപനവുമായി യോജിക്കാത്തത്?

1. ആവര്‍ത്തനസങ്കലനത്തിലൂടെ
2. ഗുണനപ്പട്ടിക ഉരുവിട്ട് പഠിച്ച
3. പുതിയസന്ദര്‍ഭങ്ങളില്‍ പ്രയോഗിച്ച്
4. പ്രായോഗിക പ്രശ്നങ്ങള്‍ നിര്‍ദ്ധാരണം ചെയ്ത്

5. കലണ്ടര്‍, അധിവര്‍ഷം

സാധാരണ വര്‍ഷവും അധിവര്‍ഷവും

• അധിവര്‍ഷത്തില്‍ അധികം ഒരു ദിവസം (365+1) ഫെബ്രുവരിയിലാണ് അധികദിനം വരിക
• മൂന്നു സാധാരണ വര്‍ഷങ്ങള്‍ക്ക് ശേഷം വരുന്നത് അധിവര്‍ഷമായിരിക്കും
• ഒരു സാധാരണ വര്‍ഷത്തില്‍ ജനുവരി ഒന്നും ഡിസംബര്‍ 31 ഉം ഒരേ ദിവസം ആയിരിക്കും . 2018 January 1 തിങ്കള്‍ 2018 December 31 തിങ്കള്‍

1997 January 1 തിങ്കള്‍ ആയാല്‍ 1998 ജനുവരി ഒന്ന് ഏതു ദിവസം ആയിരിക്കും ?

1. ചൊവ്വ
2. ബുധന്‍
3. തിങ്കള്‍
4. ഞായര്‍
• അധിവര്‍ഷം ആരംഭിക്കുന്നതിന്റെ ( ജനുവരി ഒന്ന് ) അടുത്ത ദിവസമായിരിക്കും ആ വര്‍ഷം അവസാനിക്കുന്നത്
  1. (1996 January 1 Friday, 1996 December 31 Saturday)
• ഒരു വര്‍ഷത്തെ നാലുകൊണ്ട് നിശേഷം ഹരിക്കാനാകുമെങ്കില്‍ അത് അധിവര്‍ഷമാണ്
• ഒരു വര്‍ഷം ഒരു നൂറ്റാണ്ട് ആണെങ്കില്‍ നാനൂറ് കൊണ്ട് നിശേഷം ഹരിക്കാനാകുമെങ്കിലേ അധിവര്‍ഷമാകൂ
• നാനൂറ് കൊണ്ട് നിശേഷം ഹരിക്കാവുന്ന വര്‍ഷങ്ങളിലെ ഡിസംബര്‍ 31 എപ്പോഴും ഞായറാഴ്ചയായിരിക്കും
• അധിവര്‍ഷത്തില്‍ അമ്പത്തിരണ്ട് ആഴ്ചകളും രണ്ട് ഒറ്റ ദിവസങ്ങളും ഉണ്ടായിരിക്കും ( ലഭിച്ച വര്‍ഷത്തിലെ ദിവസങ്ങളെ ഏഴുകൊണ്ട് ഹരിച്ചാല്‍ കിട്ടുന്ന ഉത്തരം )
• സാധാരണവര്‍ഷത്തില്‍ അമ്പത്തിരണ്ട് ആഴ്ചകളും ഒരു ഒറ്റ ദിവസവും ഉണ്ടായിരിക്കും

ചോദ്യങ്ങളുടെ സ്വഭാവം

1. കൂട്ടത്തില്‍ പെടാത്ത വര്‍ഷം ഏത്? ( അധിവര്‍ഷവും അല്ലാത്തവയുമായിരിക്കും നല്‍കിയിട്ടുളളത്. ഏതാണ് അധിവര്‍ഷം അല്ലെങ്കില്‍ സാധാരണവര്‍ഷം എന്നു കണ്ടെത്തി ഉത്തരത്തിലെത്താം )
2. കൂട്ടത്തില്‍ പെടാത്ത മാസമേത്? ജനുവരി , സെപ്തംബര്‍, മാര്‍ച്ച്, മെയ്. ( തുല്യദിനങ്ങളുളള മാസവും അല്ലാത്തവയുമായിരിക്കും തന്നിട്ടുണ്ടാവുക. അത് കണ്ടെത്തി ഉത്തരത്തിലെത്താം)
3. മാസജോഡികളെ കണ്ടെത്തുക (തുല്യ ദിനങ്ങളുളള മാസങ്ങളുടെ ജോഡിയും അല്ലാത്തവയും വേറിട്ടും ഇടകലര്‍ത്തിയും തരും )
4. ഫെബ്രുവരി മാസത്തില്‍ 29ദിവസങ്ങളുളള വര്‍ഷം ( അധിവര്‍ഷമേതെന്നു കണ്ടെത്തണം )
5. നിശ്ചിത വര്‍ഷത്തെ അടുത്തടുത്ത മൂന്നോ നാലോ മാസങ്ങളിലെ ആകെ ദിവസങ്ങള്‍ എത്ര? ( ഓരോ മാസത്തെയും പ്രത്യേകം എഴുതി കൂട്ടണം. ഫെബ്രുവരി മാസം ഉണ്ടെങ്കില്‍ അധിവര്‍ഷമാണോ എന്നും നോക്കണം )
6. ഒരു മാസത്തിലെ 28 -ാം തീയതി തിങ്കളാഴ്ചയാണ്. ആ മാസത്തില്‍ എത്ര ചൊവ്വാഴ്ചകള്‍ കാണും? ( ഏതൊരു ഇംഗ്ലീഷ് മാസത്തിലെയും 29,30,31 വരുന്ന ആഴ്ചകള്‍ ആ മാസം അഞ്ചെണ്ണം കാണും. അതിനാല്‍ ചൊവ്വാഴ്ചകളുടെ എണ്ണം 5. ഇവിടെ )
7. എല്ലാവര്‍ഷത്തെയും മാര്‍ച്ച്- നവംബര്‍, ഏപ്രില്‍ - ജൂലൈ, സെപ്തംബര്‍- ഡിസംബര്‍ എന്നിവ ജോഡി മാസങ്ങളായിരിക്കും. അതായത് ദിവസവും തീയതിയും സമമായിരിക്കും. ആദ്യമാസത്തെ (മാര്‍ച്ച്) കലണ്ടര്‍ നവംബറിലും ഉപോയിഗിക്കാം. മാസപ്പേര് മാത്രം വ്യത്യാസം
8. ഒരേ കലണ്ടര്‍ വരുന്ന മാസങ്ങളേവ? ( പല സാധ്യതകള്‍ തരും അതില്‍ നിന്നും ശരിയായത് കണ്ടെത്തണം . ശരി സാധ്യതകളിവയാണ്. മാര്‍ച്ച്- നവംബര്‍, ഏപ്രില്‍- ജൂലൈ, സെപ്തംബര്‍-ഡിസംബര്‍, സാധാരണ വര്‍ഷത്തില്‍ ഒക്ടോബര്‍- ജനുവരി, അധിവര്‍ഷത്തില്‍ ജനുവരി -ജൂലൈ)

ചുവടെ കൊടുത്തിരിക്കുന്നവയില്‍ ഏതെല്ലാം മാസങ്ങള്‍ക്കാണ് ഒരേ കലണ്ടര്‍ ഉപയോഗിക്കാന്‍ പറ്റാത്തത് ?
1. ഏപ്രില്‍-ജൂലൈ,
2. മാര്‍ച്ച്-നവംബര്‍,
3. ജനുവരി- മാര്‍ച്ച്
4. സെപ്തംബര്‍- ഡിസംബര്‍

9. തുല്യകലണ്ടര്‍ മാസങ്ങളിലൊന്നിലെ ദിവസം സൂചിപ്പിച്ച് മറ്റേമാസത്തെ തീയതി തന്ന് ദിവസം ചോദിക്കല്‍ ( ഉദാഹരണം മാര്‍ച്ച് എട്ട് ചൊവ്വാഴ്ചയായാല്‍ നവംബര്‍ പത്ത് ഏതുദിവസം ആയിരിക്കും.? തുല്യകലണ്ടറായതിനാല്‍ വ്യാഴം എന്നു കണ്ടെത്താം)

6. ഭിന്നങ്ങളുടെ സങ്കലനവും വ്യവകലനവും

1. സമാനഛേദക ഭിന്നങ്ങളാണെങ്കില്‍ അതേ ഛേദം എഴുതി അംശങ്ങള്‍ തമ്മില്‍ കൂട്ടുകയോ വ്യത്യാസം കാണുകയോ ചെയ്താല്‍ മതി

1. 
   
   

   
   

   • ഛേദം വ്യത്യസ്തമാണെങ്കില്‍ സമഛേദീകരിച്ചശേഷം അംശങ്ങള്‍ തമ്മില്‍ കൂട്ടുകയോ വ്യത്യാസം കാണുകയോ ചെയ്താല്‍ മതി

   

1. രണ്ടു മിശ്രഭിന്നങ്ങള്‍ തമ്മിലാണെങ്കില്‍ വിഷമഭിന്നമാക്കി മുകളില്‍ സൂചിപ്പിച്ചവയില്‍ അനുയോജ്യമായ രീതി ഉപയോഗിച്ച് ക്രിയചെയ്യുക

ഭിന്നങ്ങളുടെ ഗുണനം

നിഗമനം രൂപീകരിക്കൂ 

 

ഭിന്നങ്ങളുടെ ഹരണം - ഒരു ഭിന്നസംഖ്യയെ മറ്റൊരു ഭിന്നസംഖ്യകൊണ്ട്ഹരിക്കുന്നതിന് രണ്ടാമത്തെ ഭിന്നസംഖ്യയുടെ വ്യുത്ക്രമം( ഭിന്നസംഖ്യയെ തലതിരിച്ചിടല്‍) കൊണ്ട് ഗുണിച്ചാല്‍ മതി.

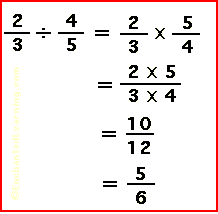
 തുല്യഭിന്നങ്ങള്‍ കണ്ടെത്താനറിയാമോ?

വ്യത്യസ്ത ഛേദമുളള ഭിന്ന സംഖ്യകളുടെ സങ്കലനം അവതരിപ്പിക്കുന്നതിന് അവശ്യം വേണ്ട മുന്നറിവ്

1. ഭിന്ന സംഖ്യകളുടെ ഗുണനം
2. ദശാംശസംഖ്യകലുടെ സങ്കലനം
3. ഒരേ അംശമുളള ഭിന്നസംഖ്യകളുടെ സങ്കലനം
4. തുല്യഭിന്നം എന്ന ആശയം

2/5നെ സംബന്ധിച്ച് ശരിയല്ലാത്ത പ്രസ്താവന ഏത്?

1. 5X2/5
2. 1/2+1/2+1/2+1/2+1/2
3. 5/4ന്റെ ഇരട്ടി
4. 8/5ന്റെ പകുതി

 BODMAS

ഒന്നിലേറെ അടിസ്ഥാനക്രിയകള്‍ ഒരുമിച്ച് വരുമ്പോള്‍ സംഖ്യാവാചകം ലഘൂകരിക്കാന്‍  BODMAS രീതി ഉപയോഗിക്കുന്നു

B-ബ്രായ്ക്കറ്റിനുളളിലെ ക്രിയ ആദ്യം ചെയ്യണം

O-of ക്രിയ ( ഇത് ഗുണനത്തെയാണ് സൂചിപ്പിക്കുന്നത്)

D- ഡിവിഷന്‍ ( ഹരണം)

M- മള്‍ട്ടിപ്ലിക്കേഷന്‍ -ഗുണനം

A- അഡീഷന്‍- സങ്കലനം

S- സബ്സ്ട്രാക്ഷന്‍ - വ്യവകലനം

64+16/2-6x7+3x2

64+16/2-42 +3x2

64+16/2-42+6

64+8-42+6

72-42+6

30+6=36

7. ശതമാനം

• ഛേദം 100 ആയിട്ടുള്ള ഒരു ഭിന്നസംഖ്യയെ ആണ് ശതമാനം എന്നു പറയുന്നത് .

• ശതമാനം(Percentage) എന്ന വാക്കിൻറെ അർത്ഥം 'നൂറിൽ ഇത്ര'(per hundred) എന്നാണ് .
• എളുപ്പത്തിൽ എഴുതുന്നതിനായി ശതമാന ചിഹ്നം (%) ഉപ യോഗിച്ച് എഴുതുന്നു.ഉദാഹരണത്തിനു 25/100 എന്നത് 25% എന്ന് എഴുതാം. ദശാംശസംഖ്യാവ്യവസ്ത ഉപയോഗിച്ച് ഇത് .25 എന്നും എഴുതാം

ഒരു സംഖ്യയുടെ 15% 9 ആയാൽ സംഖ്യ ?

• a) 135  b) 9/15   c) 15/9   d) 60

  സംഖ്യ a ആയാൽ

a x (15/100) = 9 
15 a = 900
  a = 900/15 = 60 (d)

25% ൻറെ 25% എത്ര ?
a) 625   b) 0.000625   c) 0.0625  d) 6.25

25/100 x 25/100 = 625/10000 = 0.0625

8. ലാഭവും നഷ്ടവും

ഒരു വസ്തു വാങ്ങിയ വിലയേക്കാൾ കൂടിയ വിലയ്ക്ക് വിറ്റാൽ ലാഭം ഉണ്ടാകുന്നു
ലാഭം = വിറ്റ വില — വാങ്ങിയ വില

1. ലാഭ ശതമാനം എത്രയാണെന്നുള്ളത് വാങ്ങിയ വിലയെ അടിസ്ഥാനപ്പെടുത്തിയാണിരിക്കുന്നത്

   ie;

   ലാഭ ശതമാനം

   =

   ലാഭം           x 100 വാങ്ങിയ വില

   ഒരു വസ്തുവിൻറെ വാങ്ങിയവില 60 രൂപയും വിറ്റവില 66 രൂപയുമായാൽ ലാഭ ശതമാനം എത്ര
   
   a) 6%       b) 10%      c) 12%          d) 20%
   
   ലാഭശതമാനം = (ലാഭം x 100)/വാങ്ങിയ വില
   
                                = (66-60)/60 x 100
   
                               = 6/60 x 100 =10% (Ans : b)
2. ഒരു വസ്തു വിറ്റ വില വാങ്ങിയ വിലയേക്കാൾ കുറവാണെങ്കിൽ നഷ്ടം ഉണ്ടാകുന്നു
   നഷ്ടം = വാങ്ങിയ വില — വിറ്റ വില
3. നഷ്ട ശതമാനം കണക്കാക്കുന്നത് വാങ്ങിയ വിലയെ അടിസ്ഥാനപ്പെടുത്തിയാണ്

ie;

നഷ്ട ശതമാനം

=

നഷ്ടം           x 100 വാങ്ങിയ വില

ഒരു മേശ 720 രൂപയ്ക്ക് വിറ്റപ്പോൾ 25% നഷ്ടം ഉണ്ടാകുന്നു. മേശയുടെ വാങ്ങിയ വില എത്ര
a) 600     b)960       c) 860       d) 900

വാങ്ങിയ വില = വിറ്റ വില \(100-നഷ്ട%) x 100

                                = 720 x 100 / (100-25)

                                = 72000\75 = 960 (Ans : b)

വിറ്റ വില = (100+ലാഭശതമാനം x വാങ്ങിയ വില)/100

വാങ്ങിയ വില = (100/(100+ലാഭശതമാനം)) x വിറ്റ വില

വാങ്ങിയ വില = (100/(100+നഷ്ടശതമാനം)) x വിറ്റ വില

50 രൂപയ്ക് വാങ്ങിയ സാധനം 60 രൂപയ്ക് വിറ്റാല്‍ ലാഭശതമാനം?

1. 10%
2. 20%
3. 5%
4. 15%

200 രൂപയ്ക് വാങ്ങിയ സാധനം 180 രൂപയ്ക് വിറ്റാല്‍ നഷ്ടശതമാനം?

1. 10%
2. 20%
3. 5%
4. 15%

120വാങ്ങിയ സാധനം 5% നഷ്ടത്തില്‍ വിറ്റാല്‍ വിറ്റവില എത്ര?

1. 115
2. 114
3. 112
4. 119

1500വിലയുളള സാധനം 20% ലാഭത്തില്‍ വിറ്റു. എത്ര രൂപയ്കാണ് വിറ്റത്?

1. 1800
2. 1700
3. 2200
4. 1600

9. ദശാംശസംഖ്യകള്‍

സംഖ്യകളെല്ലാം തന്നെ പത്തിന്റെ (10) അനുക്രമമായ ഘാത(ഗുണിത)ങ്ങളാണെന്ന് പ്രത്യേകം ഓര്‍മിക്കേണ്ടതുണ്ട്.

അതായത് ഓരോ സ്ഥാനം ഇടത്തോട്ട് പോകും തോറും പത്ത് മടങ്ങ് വില വര്‍ധിക്കും വലത്തോട്ടാണ് പോകുന്നതെങ്കില്‍ വില പത്തിലൊന്നായി കുറയും

നൂറ്, പത്ത്, ഒന്ന്, പത്തിലൊന്ന്, നൂറിലോന്ന് എന്നതിന്റെ യുക്തി മനസിലായല്ലോ.

ദശത്തെ ( പത്തിനെ) ആധാരമാക്കുകയാണ് .ഒന്നിനെ ദശമായി അംശിച്ചപ്പോള്‍ ദശാംശമായി.

70000കിട്ടണമെങ്കില്‍ 700നോട് എത്ര നൂറു കൂട്ടണം?

• 693,6930,69300,70000

20 നോട് എത്രപത്തുകള്‍ കൂട്ടിയാല്‍ 70000കിട്ടും?

• 6998,69980,6980,7000

6464എന്ന സംഖ്യയില്‍ എത്ര 64 ഉണ്ട്

• 64,11,101,1

ഒരു ഭിന്നസംഖ്യയെ സമാനമായ ഒരു ദശാംശ സംഖ്യയാക്കി മാറ്റുന്നതിന് അംശത്തെ ച്ഛേദം കൊണ്ട് ഹരിച്ചാല്‍ മതി.
1/4 = 0.25, 1/2 = 0.5

രണ്ട് ദശാംശ സംഖ്യകള്‍ തമ്മില്‍ കൂട്ടണമെങ്കില്‍ അവയുടെ ദശാംശസ്ഥാനങ്ങളുടെ എണ്ണം തുല്യമായിരിക്കണം. എണ്ണം തുല്യമല്ലെങ്കില്‍ പൂജ്യം ചേര്‍ത്ത് സ്ഥാനങ്ങളുടെ എണ്ണം തുല്യമാക്കണം. ഇതേ രീതിയില്‍തന്നെ വ്യവകലനവും ചെയ്യാന്‍ കഴിയും
0.3+ 0.8 = 1.1
5.4 - 2.68 = ?

ദശാംശസംഖ്യയെ 10,100,1000 മുതലായ സംഖ്യകള്‍ കൊണ്ട് ഗുണിക്കാന്‍ ഗുണിക്കേണ്ട സംഖ്യയില്‍ എത്ര പൂജ്യങ്ങള്‍ ഉണ്ടോ അത്രയും സ്ഥനം ദശാംശ ബിന്ദുവിനെ വലത്തോട്ട് നീക്കുക.

6.74 x10 =67.4
9.52 x 100 = 952

രണ്ടോ അതിലധികമോ ദശാംശ സംഖ്യകള്‍ തമ്മില്‍ ഗുണിക്കുന്പോള്‍ അവയുടെ ദശാംശസ്ഥാനങ്ങളുടെ എണ്ണവും ഗുണനഫലത്തിലെ ദശാംശസ്ഥാനങ്ങളുടെ എണ്ണവും തുല്യമായിരിക്കും.
.6.3 x 2.5 = 16.38

ദശാംശസംഖ്യയെ 10, 100, 1000 മുതലായ സംഖ്യകള്‍ കൊണ്ട് ഹരിക്കുന്നതിന് ദശാംശ ബിന്ദുവിന്‍റെ ഹാരകത്തില്‍ എത്ര പൂജ്യങ്ങള്‍ ഉണ്ടോ അത്രയും സ്ഥാനം ഇടത്തോട്ട് നീക്കുക.
6.4 ÷ 10 = 0.64
10.6 ÷ 100 = 0.106 

ദൂരവും സമയവും

എല്ലാ പരീക്ഷകളിലും ഗണിത വിഭാഗത്തില്‍ ചോദിച്ചു കാണുന്ന ഒരു ചോദ്യ ഇനം ആണ്  ദൂരവും സമയവും
പ്രധാനമായും 4 ടൈപ്പ് ചോദ്യങ്ങളാണ് ഈ വിഭാഗത്തില്‍ നിന്നും
ഓർത്തിരിക്കേണ്ട സൂത്രവാക്യങ്ങൾ:
    • സമയം കാണാൻ = ദൂരം/വേഗം.
    • ദൂരം കാണാൻ = സമയംxവേഗത.
    • വേഗത കാണാൻ = ദൂരം/സമയം.
    • Km/hr നെ m/s ആക്കാൻ = 5/18 കൊണ്ട് ഗുണിക്കുക
    • ഒരു വസ്തതു ഒരു യൂണിറ്റ് സമയത്തിൽ സഞ്ചരിക്കുന്ന ദൂരത്തെയാണ് വേഗത എന്നു പറയുന്നത്. ഒരു കാർ 1 മണിക്കുറിൽ 22 കിലോമീറ്റർ ദൂരം സഞ്ച രിക്കുന്നുവെങ്കിൽ ആ കാറിന്റെ വേഗത 22 കി.മീ/ മണിക്കുർ ആണ്. വേഗതയുടെ യൂണിറ്റ് സാധാരണയായി km/hr (kilometre/hour), m/sec (metre/second) എന്നീ യൂണിറ്റുകളിലാണ് പറയുന്നത്.
ഉദാഹരണമായി : 25m/sec എന്നത്കൊണ്ട് അർത്ഥമാക്കുന്നത് ഒരു സെക്കന്റിൽ 25 മീറ്റർ ദൂരം സഞ്ചരിക്കുന്നു എന്നതാണ്.
        ◦ 35 km/hr - ഒരു മണിക്കുറിൽ 35 കിലോമീറ്റർ ദൂരം സഞ്ചരിക്കുന്നു.
        ◦ 500m/min - ഒരു മിനുട്ടിൽ 500 മീറ്റർ ദൂരം സഞ്ചരിക്കുന്നു.
    1. 120 മീറ്റർ നീളമുള്ള ഒരു തീവണ്ടി ഫ്ളാറ്റ്‌ഫോമിൽ നിൽക്കുന്ന ഒരാളെ കടന്നുപോകാൻ സഞ്ചരിക്കേണ്ട ദൂരം ?
(a)240 മീറ്റർ (b)120 മീറ്റർ (c )360 മീറ്റർ (d)0 മീറ്റർ
ഉത്തരം (b)
ട്രെയിനിന്റെ നീളം തന്നെയായിരിക്കും ഒരാളെ കടന്നുപോകാൻ സഞ്ചരിക്കേണ്ട ദൂരം. അതായത് 120 മീറ്റർ ( വിളക്കുകാല്‍, മറ്റു സ്ഥിര വസ്തുക്കള്‍ എന്നിവ വെച്ച് ഇത്തരം ചോദ്യം ചോദിക്കാം )
    2. തീവണ്ടിയും പാലവും . ഒരു തീവണ്ടി പാലം കടന്നു പോകുന്നതിന് സഞ്ചരിക്കേണ്ട ദൂരം എന്നത് പാലത്തിന്റെയും തീവണ്ടിയുടെയും നീളമാണ്. രണ്ടും തമ്മില്‍ കൂട്ടിയാല്‍ മതി.
230 മീറ്റർ നീളമുള്ള ഒരു തീവണ്ടിക്ക് 140 മീറ്റർ നീളമുള്ള ഒരു പാലം കടന്നുപോകാൻ സഞ്ചരിക്കേണ്ട ദൂരം എത്ര?
(a) 235 മീറ്റർ (b) 370 മീറ്റർ (c ) 250 മീറ്റർ (d) 350 മീറ്റർ
ഉത്തരം: (b)
ദൂരം = തീവണ്ടിയുടെ നീളം +പാലത്തിന്റെ നീളം = 230 140 = 370 മീറ്റർ
    3. ഓരു തീവണ്ടിക്ക് മറ്റൊന്നിനെ കടന്നുപോകുന്നതിന് ( സമാനദിശയിലാണെങ്കിലും ഏതിര്‍ ദിശയിലാണെങ്കിലും) രണ്ടു വണ്ടികളുടെയും നീളങ്ങളുടെ തുക കണ്ടാല്‍ മതി.
    4. രണ്ടു ട്രെയിനുകള്‍ ഒരേ ദിശയില്‍ സഞ്ചരിക്കുമ്പോള്‍ അവയുടെ ആപേക്ഷിക വേഗത ട്രെയിനുകളുടെ വേഗതകളുടെ വ്യത്യാസമായിരിക്കും. വിപരീതദിശയിലാണെങ്കില്‍ ട്രെയിനുകളുടെ വേഗതകളുടെ തുകയായിരിക്കും.
    5. ഒരു തീവണ്ടി ഒരു പാലം / പ്ലാറ്റ്ഫോം കടന്നു പോകാൻ എടുക്കുന്ന സമയം
തീവണ്ടിയുടെ നീളം +പാലത്തിന്റെ നീളം/വേഗത
    6. ഒരു തീവണ്ടി ഇലക്ട്രിക് പോസ്റ്റ് കടന്നു പൊകാനെടുക്കുന്ന സമയം  = തീവണ്ടിയുടെ നീളം / വേഗത
    7. ഒരു വാഹനം 2 മണിക്കൂർകൊണ്ട് 48 കി.മീ. ദൂരം സഞ്ചരിക്കുന്നുവെങ്കിൽ ഈ വാഹനത്തിന്റെ വേഗത എന്ത് ?
2 മണിക്കൂർ കൊണ്ട് സഞ്ചരിക്കുന്ന ദൂരം
= 48 കി . മീ
1 മണിക്കൂർകൊണ്ട് സഞ്ചരിക്കുന്ന ദൂരം = 48/2 = 24 കി.മീ
വേഗത = 24 km/hr
       ഇവിടെ സഞ്ചരിക്കുന്ന ദൂരത്തെ സഞ്ചരിക്കാനെടുത്ത സമയം കൊണ്ട് ഹരിച്ചപ്പോൾ വേഗത കിട്ടി. അതായത്
വേഗത = ദൂരം / സമയം
സമയം = ദൂരം / വേഗത
ദൂരം = വേഗത സമയം
    8. 200 കി .മീ. ദൂരം 8 മണിക്കൂർകൊണ്ട് യാത്രചെയ്യുന്ന ഒരു കാറിന്റെ വേഗത എന്ത് ?
വേഗത = 200km/8 hr = 25 Km/hr
    9. ഒരാൾ 8 കി.മീ /മണിക്കൂർ വേഗതയിൽ സൈക്കിൾ ചവിട്ടുന്നുവെങ്കിൽ അഞ്ചര മണിക്കൂർകൊണ്ട് അയാൾ എത്ര ദൂരം സഞ്ചരിക്കും ?
ദൂരം = വേഗത Xസമയം
= 8 X 5.5 = 44 കി മി
    10. ഒരേ ദൂരം രണ്ടു വ്യത്യസ്ത വേഗതയില്‍ (a &b) സഞ്ചരിച്ചുവെങ്കില്‍ ശരാശരി വേഗത =2ab/ a+b 
ഉദാ-ഒരാൾ Xൽ നിന്നും Yലേക്ക് 40km/hr വേഗതയിലും തിരിച്ച് ൽ നിന്നും ലേക്ക് 60km/hr വേഗതയിലും സഞ്ചരിക്കുന്നു. എങ്കിൽ ആകെ യാത്രയിലെ ശരാശരി വേഗത എത്ര ?
(a)50km/hr (b)55km/hr
(c )48 km/hr (d)50km/hr
ഉത്തരം (c ) a=40,b=60
2ab/ ab = 2x40x60/40+60
= 2x40x60/100 = 48 km/hr
    11. യുണിറ്റ് മാറ്റം ഒരേ ചോദ്യത്തിൽ വ്യത്യസ്ത യൂണിറ്റുകൾ തന്നിരുന്നാൽ ഏതെങ്കിലും ഒരു യൂണിറ്റിലേക്കു കൊണ്ടു വന്നു വേണം ക്രിയകൾ ചെയ്യാൻ
km/hr നെ m/sec ആക്കാൻ 5/18 കൊണ്ട് ഗുണിക്കണം.
m/ sec-നെ km/hr ആക്കാൻ 18/5 കൊണ്ട് ഗുണിക്കണം.
km/hr-നെ m/min ആക്കാൻ 50/3 കൊണ്ട് ഗുണിക്കണം.
m/min-നെ km/hr ആക്കാൻ 3/50 കൊണ്ട് ഗുണിക്കണം.
m/min-നെ m/sec ആക്കാൻ 1/60 കൊണ്ട് ഗുണിക്കണം
m/sec-നെ m/min ആക്കാൻ 60 കൊണ്ട് ഗുണിക്കണം
    12. 15 m /sec വേഗതയിലോടുന്ന ഒരു തീവണ്ടി 3 മണിക്കൂർ കൊണ്ട് എത്ര ദൂരം സഞ്ചരിക്കും ?
(a)168km (b)162Km (c )180km (d)200km
ഉത്തരം (d)
15 m/sec - നെ km/hr ലേക്ക് മാറ്റുക .
… 15x 18/5 = 54km/hr
1 മണിക്കൂറിൽ തീവണ്ടി സഞ്ചരിച്ച ദൂരം = 54 km
3 മണിക്കൂറിൽ തീവണ്ടി സഞ്ചരിച്ച ദൂരം =543
= 162 km
    13. ചുവടെ കൊടുത്തിരിക്കുന്നവയിൽ ഏറ്റവും കൂടുതൽ വേഗതയിൽ ഓടുന്ന തീവണ്ടി ഏത്?
(a) 2.5m/sec (b) 72km/hr. (c ) 500 m/min (d) മൂന്നിനും തുല്യ വേഗത
ഉത്തരം (a)
(ഇവിടെ മൂന്ന് ഓപ്ഷനുകളും ഒരേ യൂണിറ്റിലേയ്ക്ക് കൊണ്ട് വന്ന് താരതമ്യം ചെയ്യണം)
(a) 2.5m/sec = 25X18/5 = 90 km/hr.
(b) 72 km/hr
(c )500 m/min = 500 3/50=30 km/hr ഇത്തരം ക്രിയകൾ വേഗത്തിൽ ചെയ്യാൻ ഉപകരിക്കും
118 = 18,218=36,318=54,418=72,518=90,618=108…'
    14. ശരാശരി വേഗത .ഒരേ ദൂരം രണ്ട് വ്യത്യസ്ത വേഗത്തിൽ സഞ്ചരിക്കുന്ന കഴിയുമ്പോഴുള്ള ശരാശരി വേഗത =2ab/ab
    15.  180 മീ നീളമുള്ള ഒരു ട്രെയിൻ 54 Km/h വേഗത്തിൽ ഓടുന്നു.പാതവക്കിലെ ഒരു പോസ്റ്റ് കടക്കാൻ തീവണ്ടിക്ക് എത്ര സെക്കന്റ വേണം?
       ◽ഇവിടെ 54 Km/h നെ m/s ആക്കണം;
◽54x5/18 = 15 m/s.
◽Time = Distance÷Speed = 180÷15
◽Ans= 12 Sec.
    16.  200 മീ നീളമുള്ള തീവണ്ടി 90 Km/h വേഗത്തിൽ ഓടുന്നു. 100 മീ നീളമുള്ള പാലം കടക്കാൻ ആ തീവണ്ടിക്ക് വേണ്ട സമയമെന്ത്?
       ◽90x5/18 = 25 m/s.
◽ദൂരം = 200+100 = 300 മീ.
◽Time = Distance÷Speed. = 300÷25
◽Ans = 12 Sec.
    17. 72 km/h ൽ ഓടുന്ന ഒരു ട്രെയിൻ ഒരു പോസ്റ്റ് കടക്കാൻ 10 സെക്കന്റ് എടുത്തു. എങ്കിൽ ട്രെയിന്റെ നീളമെന്ത്?
       ◽72x5/18 = 20m/s.
◽ട്രെയിന്റെ നീളം ചോദിച്ചാൽ 'ദൂരം' കാണാനുള്ള equation ഉപയോഗിക്കാം:
◽Distance = Time x Speed.
◽=10 x 20. Ans = 200 മീറ്റർ.

    18. 150 മീ നീളമുള്ള ഒരു ട്രെയിന് വഴിയരുകിലെ പോസ്റ്റ് കടന്ന് പോകാൻ 10 സെക്കന്റ് എടുത്തു. If, 350 മീ നീളവുള്ള ഒരു പാലം കടക്കാൻ എത്ര സമയം വേണം?
       ◽Equation: Time = Distance/Speed.
       ◽ഇവിടെ ദൂരമെന്നത് 500 മീ ആണ്. but വേഗത തന്നിട്ടില്ല. അതാദ്യം കാണണം:
◽= 150 മീ നീളമുള്ള ട്രെയിൻ 10 Sec കൊണ്ട് പോസ്റ്റ് കടന്നു പോയി. Then ◽ട്രെയിന്റെ വേഗത: 150/10 = 15 m/s.
◽ഇനി ആകെ ദൂരം: 150+350 = 500 മീ.
◽Answer = 500/15 = 33 1/3 Sec വേണം.

    19. ഒരേദിശയിലും, എതിർദിശയിലും ഓടുന്ന തീവണ്ടി കണക്ക്.

150 മീ നീളമുള്ള ട്രെയിൻ 58 km/h ൽ ഓടുന്നു.4 km/hr ൽ അതേ ദിശയിലോടുന്ന ഒരാളെ മറികടക്കാൻ തീവണ്ടിക്ക് എന്ത് സമയം വേണം?
       ◽നീളം/ദൂരം = 150 മീ.
◽ഓടുന്നയാൾ ഒരേദിശയിലായതിനാൽ വേഗം = 58 - 4 = 54 km/hr.
◽=54x 5/18 = 15 m/s.
◽സമയം = ദൂരം/വേഗം. ;150/15
◽= Ans 10 Sec വേണം.

    20. 180 മീ നീളമുള്ള ട്രെയിൻ 60km/hr ൽ ഓടുന്നു.3 km/hr ൽ എതിർദിശയിലോടുന്ന ഒരാളെ മറികടക്കാൻ തീവണ്ടിക്ക് എന്ത് സമയം വേണം?
       ◽നീളം/ദൂരം = 180 മീ.
◽ഓടുന്നയാൾ എതിർദിശയിലായതിനാൽ വേഗം = 60 + 3= 63 km/hr.
◽=63x 5/18 = 17.5 m/s.
◽സമയം = ദൂരം/വേഗം. ;180/17.5
◽= Ans 10 2/7 sec വേണം.
 

തുടരും

സാമ്പത്തികനേട്ടത്തോടെ കെ ടെറ്റ് പരിശീലനം നടത്തുന്ന സ്ഥാപനങ്ങളും വ്യക്തികളും ഈ കുറിപ്പുകള്‍ ഉപയോഗിക്കരുതെന്ന് അഭ്യ‍ർഥന

മറ്റു ലക്കങ്ങള്‍ വായിക്കാന്‍
വിശദമായ കുറിപ്പുകള്‍

1. കെ ടെറ്റ് /PSC പഠനസഹായി.1
2. കെ ടെറ്റ് പഠനസഹായി 2
3. കെ ടെറ്റ് /PSCപഠനസഹായി -3
4. കെ ടെറ്റ്/ PSC പഠനസഹായി -4 ( ബുദ്ധി സിദ്ധാന്തങ്ങ...
5. കെ ടെറ്റ്/ PSC പഠനസഹായി 5 ( സാമൂഹിക ജ്ഞാനനിര്‍മിത...
6. കെ ടെറ്റ്/ PSC പഠനസഹായി 6 ( ജ്ഞാനനിര്‍മിതി വാദം)
7. കെ ടെറ്റ് /PSC പഠനസഹായി 7 ( സമഗ്രതാദര്‍ശനം) 
8. കെ ടെറ്റ് /PSC പഠനസഹായി 8 ( വ്യവഹാരവാദം)
9. കെ ടെറ്റ് /PSC പഠനസഹായി 9 ( സന്മാര്‍ഗവികാസം)  
10. കെ ടെറ്റ് /PSC പഠനസഹായി 10 (വ്യക്തിത്വം)
11. കെ ടെറ്റ് /PSC പഠനസഹായി 11,12  
12. ടെറ്റ് /PSC പഠനസഹായി 13,14
13. കെ ടെറ്റ്/ PSC പഠനസഹായി 15 
14. കെ ടെറ്റ്/ PSC പഠനസഹായി 16 ( മലയാളം) 
15. കെ ടെറ്റ് /PSC പഠനസഹായി 17 
16. കെ ടെറ്റ് /PSC പഠനസഹായി 18 (ശാസ്ത്രം) 
17. കെ ടെറ്റ് /PSC പഠനസഹായി 19 ( ഗണിതം) 
18. കെ ടെറ്റ് /PSC പഠനസഹായി 20( ഗണിതം) 
19. കെ ടെറ്റ് /PSC പഠനസഹായി 22 (ശാസ്ത്രം)